Photonics is at the core of the technological revolution in telecommunications. It is situated in the overlap of three basic scientific disciplines that carry the present technological development: electronics, optics, and solid-state physics. The extent of research and investment in optoelectronics is rising explosively worldwide. Photonic devices are essential for the envisioned hybrid optoelectronic computer and high-speed, high throughput information technologies. CompsLight is at the leading edge of research activities in this interdisciplinary field.
A new paradigm has emerged in the past decades that links the fundamental concepts of the micro-world of quantum solid-state physics and the macro-world of classical wave physics. A new type of photonic structure, photonic crystal, has been suggested and demonstrated experimentally for controlling electromagnetic waves in three dimensions. Photonic crystals can be viewed as an optical analog of semiconductors, in the sense that they modify the propagation characteristics of light, just as an atomic lattice modifies the properties of electrons through the band gap structure [1].
One of the realizations of photonic crystals is photonic lattices. Such structures represent optical waveguide arrays with periodic modulation in the refractive index, where the refractive index contrast is lower than in photonic crystals, and they are suitable for the investigation of discrete effects and other collective phenomena. Such structures have examples ranging from simple one-dimensional Bragg gratings and waveguide arrays [2] over two-dimensional photonic crystal fibers [3] to more complex three-dimensional photonic crystals that are known to exist in different geometries [4]. The important common feature of all these structures is the ability to manipulate the flow of light in the direction of periodicity. To further increase the light control possibilities, the effects of nonlinearity and periodicity can be combined in nonlinear photonic crystals [5]. An important example is given by the discrete soliton as a localized wavepacket arising from the balance between diffraction (or dispersion) and nonlinearity which has been observed in both one- and two-dimensional geometries [6].
Until now, several different approaches for the fabrication of photonic crystals exist, including the use of arrays of optical fibers and writing optical waveguides in bulk glasses using femtosecond laser beams. Although these mechanisms enable precise material structuring with periodicities adequate for optical waves, they do not allow for flexible changes of structural parameters (e.g., lattice period or modulation depth). In contrast, the optical induction in photorefractive crystals [7] provides highly reconfigurable, wavelength-sensitive nonlinear structures which can be induced at very low power levels.
The optical induction technique, we are planning to use, allows an arbitrary dynamical structuring of photorefractive materials so that different lattice configurations and sizes can be generated and can be created (or erased) with no difficulty. The basic idea of the optical induction technique is to modulate the refractive index of nonlinear material by external illumination (photorefractive effect). The linearly polarized laser beam is spatially modulated to encode the lattice structure by a spatial light modulator (SLM), thus inducing refractive index modulation into the biased photosensitive crystal which is a unique way to generate dynamical photonic lattices in the crystal: changing the encoding on SLM modifies photonic structure in the crystal allowing for the photorefractive response time.
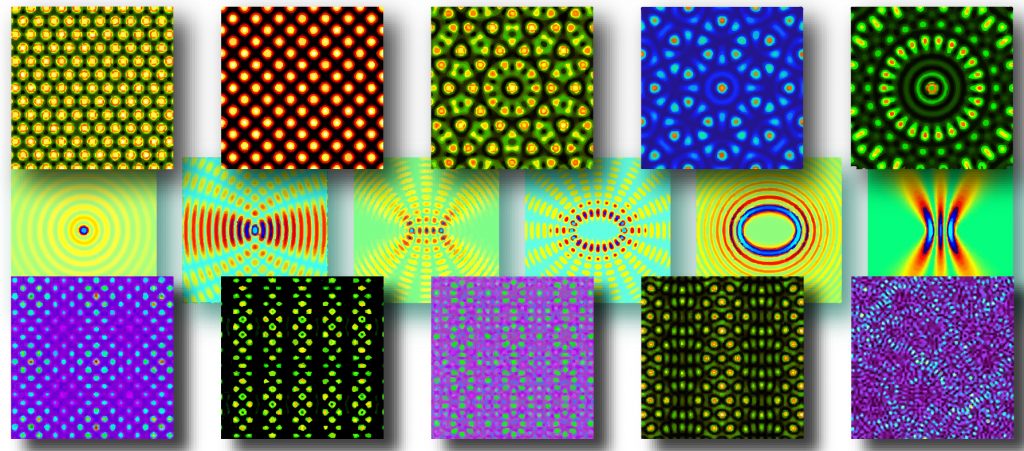
Specific geometry in which light propagates along with waveguide arrays with moderate modulation of the refractive index allows us to model such systems with paraxial approximation. The paraxial equation is formally identical to the time-dependent Schrödinger equation, where the role of the time is played by propagation dimension, mass by k vector, and quantum wave function by envelope amplitude. Then relative structural stability of solid-state crystal lattices in time corresponds to waveguide arrays preserved along propagation coordinate. Non-diffracting beams [8] are an ideal candidate for the generation of photonic structures homogenous in one dimension.
Up to now, periodic photonic structures have led to light control by photonic band gaps in space and time, whereas random photonic structures give rise to localization [9]. Dynamical control and manipulation of light by deterministic aperiodic or complex photonic structures [10] at the intersection between periodic and random crystal structures have not yet been fully understood nor exploited for applications. The richness of aperiodic structures provides significant flexibility in engineering the optical response for applications in future devices. Therefore, the CompsLight project will focus on the theoretical and experimental realization of different novel kinds of deterministic aperiodic photonic lattices (DAPL) created by different combinations of non-diffracting beams, combining them in metastructures, splicing in both transverse dimensions in different offsets thus allowing for the tunable optical response. Building on top of these tailored metastructures, their randomization allows for an additional level of diffraction control. The propagation of light in such advanced (exotic) structures is a rather unexplored topic, and will thus be thoroughly investigated in this proposal.
[1] J.D. Joannopoulos, R.D. Meade, and J.N. Winn, Photonic Crystals: Molding the Flow of Light (Princeton University Press, Princeton N.J., 1995)
[2] P. Yeh, Optical Waves in Layered Media, Wiley, New York (1998)
[3] P.S.J. Russell, Photonic crystal fibers, Science 299, 358 (2003)
[4] S.Y. Lin, J.G. Fleming, D.L. Hetherington, B.K. Smith, R. Biswas, K.M. Ho, M.M. Sigalas, W. Zubrzycki, S.R. Kurtz, J. Bur, A three-dimensional photonic crystal operating at infrared wavelengths, Nature 394, 251, 1998
[5] S.F. Mingaleev, Y.S. Kivshar, Nonlinear photonic crystals: toward all-optical technologies, Opt. Photon. News 13, 48 (2002)
[6] J.W. Fleischer, M. Segev, N.K. Efremidis, D.N. Christodoulides, Observation of two dimensional discrete solitons in optically induced nonlinear photonic lattices, Nature 422, 147 (2003)
[7] N.K. Efremidis, S. Sears, D.N. Christodoulides, J.W. Fleischer, and M. Segev, Discrete solitons in photorefractive optically induced photonic lattices, Phys. Rev. E 66, 046602 (2002)
[8] M. V. Berry and N. L. Balazs, Nonspreading wave packets, Am. J. Phys. 47, 264 (1979)
[9] T. Schwartz, G. Bartal, S. Fishman, and M. Segev, Transport and Anderson localization in disordered two-dimensional photonic lattices, Nature 446, 52–55 (2007)
[10] Z.V. Vardeny, A. Nahata, and A, Agrawal, Optics of photonic quasicrystals, Nature Photonics 7, 177 (2013)




